Чему равен стандартный коэффициент головки ножки зуба для нормальной цилиндрической передачи
Опубликовано: 23.04.2024
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.

Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Цилиндрические зубчатые передачи.
Расчет геометрических параметров
Термины и обозначения приведены в табл. 1, определения терминов см. ГОСТ 16530—83 и 16531-83.
1. Термины и обозначения цилиндрических зубчатых передач
Делительное межосевое расстояние - a
Межосевое расстояние - aw
Ширина венца цилиндрического зубчатого колеса - b
Рабочая ширина венца зубчатой передачи - bw
Радиальный зазор пары исходных контуров - c
Коэффициент радиального зазора нормального исходного контура – c*
Высота зуба цилиндрического зубчатого колеса - h
Высота делительной головки зуба цилиндрического зубчатого колеса - ha
Коэффициент высоты головки исходного контура – ha *
Высота до хорды зуба колеса - h a
Высота до постоянной хорды зуба - h c
Высота до хорды дуги окружности - h ay
Глубина захода зубьев колеса, а также глубина захода зубьев исходных реек - h d
Высота делительной ножки зуба колеса - hf
Граничная высота зуба колеса - hl
Делительный диаметр зубчатого колеса - d
Диаметр вершин зубьев колеса - da
Основной диаметр зубчатого колеса - db
Диаметр впадин зубчатого колеса - df
Диаметр окружности граничных точек зубчатого колеса - dl
Начальный диаметр зубчатого колеса - dw
Радиус зубчатого колеса - r
Расчетный модуль цилиндрического зубчатого колеса - m
Нормальный модуль зубьев - mn
Окружной модуль зубьев (торцовый) - mt
Шаг эвольвентного зацепления - pb
Нормальный шаг зубьев рейки - pn
Торцовый шаг зубьев рейки - pt
Осевой шаг зубьев рейки - px
Основной нормальный шаг зубьев - pbn
Основной окружной шаг зубьев - pbt
Основная нормальная толщина зуба - sbn
Постоянная хорда зуба - s c
Нормальная толщина зуба рейки - sn
Осевая толщина зуба рейки - sx
Торцовая толщина зуба рейки - st
Толщина по хорде зуба - s
Окружная толщина на заданном диаметре dy - sty
Толщина по хорде - s y
Длина обшей нормали зубчатого колеса - W
Коэффициент смещения исходного контура - x
Коэффициент наименьшего смещения исходного контура - xmin
Коэффициент суммы смещений хΣ
Коэффициент воспринимаемого смещения - у
Коэффициент уравнительного смещения - Δу
Число зубьев зубчатого колеса (число зубьев секторно -зубчатого колеса) - z
Наименьшее число зубьев, свободное от подрезания - zmin
Число зубьев в длине обшей нормали - zw
Нормальный боковой зазор эвольвентной цилиндрической зубчатой передачи - jn
Эвольвентный угол профиля зуба – inv a
Эвольвентный угол, соответствующий точке профиля на окружности dy – inv ay
Частота вращения зубчатого колеса в минуту - n
Угол профиля зуба исходного контура в нормальном сечении - a
Угол профиля зуба в торцовом сечении - at
Угол зацепления - atw
Угол профиля в точке на концентрической окружности заданного диаметра dy - ay
Угол наклона линии зуба соосной цилиндрической поверхности диаметра dy - βy
Угол наклона линии зуба - β
Основной угол наклона линии зуба (косозубого колеса на его основном цилиндре) - βb
Угол развернутости эвольвенты зуба - v
Половина угловой толщины зуба - ψ
Половина угловой толщины зуба эквивалентного зубчатого колеса, соответствующая концентрической окружности диаметра dy /cos 2 βy - ψyv
Угловая скорость - ω
Шестерня - зубчатое колесо передачи с меньшим числом зубьев, колесо - с большим числом зубьев. При одинаковом числе зубьев зубчатых колес передачи шестерней называют ведущее зубчатое колесо, а колесом - ведомое. Индекс 1 - для величин, относящихся к шестерне, индекс 2 - относящихся к колесу.
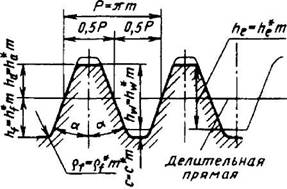
Рис. 1. Исходный контур зубчатых цилиндрических колес эвольвентного зацепления по ГОСТ 13755-81 и конических колес с прямыми зубьями по ГОСТ 13754-81
Индекс n - для величин, относящихся к нормальному сечению, t - к окружному (торцовому) сечению. В тех случаях, когда не может быть разночтения и неясности, индексы n и t можно исключить.
Термины параметров нормального исходного контура и нормального исходного производящего контура, выраженных в долях модуля нормального исходного контура, образуют добавлением слова «коэффициент» перед термином соответствующего параметра.
Обозначения коэффициентов соответствуют обозначениям параметров с добавлением знака «*», например коэффициент радиального зазора пары исходных контуров с *.
Модули (по ГОСТ9563—60). Стандарт распространяется на эвольвентные цилиндрические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанавливает:
для цилиндрических колес - значения нормальных модулей;
для конических колес - значения внешних окружных делительных модулей.
Числовые значения модулей:
1. При выборе модулей ряд 1 следует предпочитать ряду 2.
2. Для цилиндрических зубчатых колес допускается:
а) в тракторной промышленности применение модулей 3,75; 4,25 и 6,5мм;
б) в автомобильной промышленности применение модулей, отличающихся от установленных в настоящем стандарте;
в) в редукторостроении применение модулей 1,6; 3,15; 6,3; 12,5м.
3. Для конических зубчатых колес допускается:
а) определять модуль на среднем конусном расстоянии;
б) в технически обоснованных случаях применение модулей, отличающихся от указанных в таблице.
4. Стандарт предусматривает применение модулей в диапазоне значений от 0,05 до 100мм.
Исходный контур цилиндрических зубчатых колес. Под исходным контуром колес (рис. 1) подразумевают контур зубьев рейки в нормальном к направлению зубьев сечении. Радиальный зазор с = 0,25m, радиус кривизны переходной кривой зуба pf = 0.4m. Допускается увеличение радиуса рfесли это не нарушает правильности зацепления, и увеличение с до 0,35m при обработке колес долбяками и шеверами и до 0,4m при шлифовании зубьев.
Для цилиндрических колес внешнего зацепления при окружной скорости более указанной в табл. 2 применяют исходный контур с модификацией профиля головки зуба (рис. 2). При этом линия модификации - прямая, коэффициент модификации hg * должен быть не более 0,45, а коэффициент глубины модификации Δ* - не более 0,02.
Рекомендуемые значения коэффициента Δ* приведены в табл. 3.
Основные элементы зубчатого зацепления указаны на рис. 3 и 4 в соответствии с обозначением по табл. 1.
Смещение колес зубчатых передач с внешним зацеплением. Чтобы повысить прочность зубьев на изгиб, снизить контактные напряжения на их поверхности и уменьшить износ за счет относительного скольжения профилей, рекомендуется производить смешение инструмента для цилиндрических (и конических) зубчатых передач, у которых z1 ≠ z2. Наибольший результат достигается в следующих случаях:
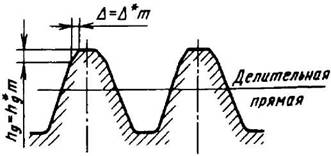
Рис. 2. Исходный контур с профильной модификацией
2. Окружная скорость колес в зависимости от их точности
Окружная скорость в м/ с при степени точности колеса по ГОСТ 1643-81
Эвольвентное зацепление двух зубчатых колес характеризуется следующим параметрами (ГОСТ 16530-70) (рис. 13.3).
Начальные окружности (dw1 и dw2) – воображаемые окружности, которые в процессе работы передачи перекатываются одна по другой без скольжения. Начальные окружности появляются у зубчатых колес в собранной передаче. Для отдельно взятого колеса понятие начальной окружности отсутствует. Оно имеет делительную окружность.
Окружность вершин зубьев (dα) – окружность ограничивающая головки зубьев.
Окружность впадин (df) – окружность, проходящая через основания впадин зубьев.
Основная окружность (db1 и db2) – окружность, при развертке которой получается эвольвента.
Делительная окружность (d1 и d2) – окружность зубчатого колеса, по которой обкатывается делительная окружность (прямая) инструмента в процессе нарезания зубьев. Делительная окружность колеса является начальной только в процессе изготовления (нарезания) зубьев. У некорригированных колес и при высотной коррекции начальные и делительные окружности совпадают.
Полюс зацепления (точка “P”) – точка касания начальных окружностей.
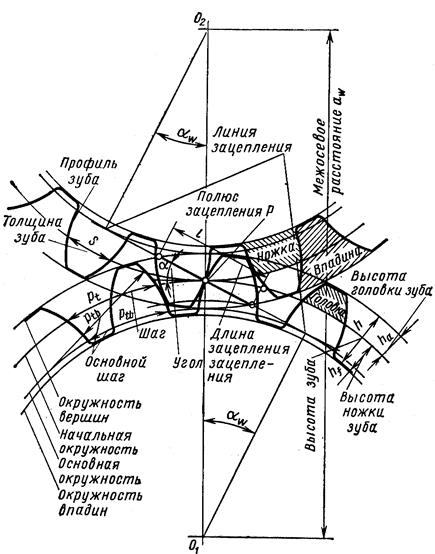
Рис. 13.3. Элементы зубчатого зацепления
Окружной шаг зацепления (Pt) – расстояние между одноименными профилями, измеренное по дуге делительной окружности, зубчатого колеса.
Головка зуба (hα) – часть зуба между делительной окружностью зубчатого колеса и его окружностью вершин зубьев.
Ножка зуба (hf) – часть зуба между делительной окружностью и его окружностью впадин.
Высота зуба (h) равна сумме высот головки и ножки зуба.
Дуга зацепления (l) – путь по начальной окружности, проходимой точкой профиля за время зацепления пары сопряженных зубьев.
Коэффициент перекрытия (ε) – отношение дуги зацепления к окружному шагу.
Линия зацепления (N1 и N2) – линия, по которой перемещается точка касания зубьев. Линия зацепления проходит через полюс зацепления и является касательной к основным окружностям.
Угол зацепления (αw) – угол между линией зацепления и касательной к начальным окружностям в полюсе зацепления.
Модуль зацепления (m). Все модули стандартизованы в пределах от 0,05 мм до 100 мм.
Рассмотренные параметры составляют определенные кинематические зависимости. В табл. 10 приводятся основные соотношения для цилиндрических некорригированных зубчатых передач внешнего зацепления.
В расчётах зуб зубчатого колеса рассматривают как балку, защемленную одним концом и нагруженную силой (Qn). Такое положение нагрузки принимается как наиболее опасное.
Наиболее опасное сечение, где наиболее вероятен излом зуба, находится у его корня в зоне наибольшей концентрации напряжений. Максимальное напряжение возникает на стороне сжатия (нерабочая сторона). Однако следует отметить то, что расчет на прочность необходимо производить по напряжению на рабочей стороне, т.к. на этой растянутой стороне зуба здесь может образоваться усталостная трещина.
Основные соотношения для цилиндрических
некорригированных зубчатых передач внешнего зацепления
| Параметры зацепления | Формулы |
| Окружной модуль |  |
| Нормальный модуль |  |
| Нормальный шаг |  |
| Межосевое расстояние |  |
| Высота головки зуба |  |
| Высота ножки зуба |  |
| Высота зуба |  |
| Радиальный зазор |  |
| Делительный диаметр |   |
| Начальный диаметр |   |
| Диаметр основной окружности |  |
| Диаметр вершин зубьев |   |
| Диаметр впадин |   |
| Коэффициент перекрытия |  |
13.3. Расчет зубьев
цилиндрических прямозубых зубчатых колес на изгиб
- для обозначения расчета на изгиб, который проводится по ножке зуба принят индекс F (от термина ножка – Fut – на английском и немецком языках).
- для обозначений расчета на контактную прочность принят индекс H, в честь автора теории расчетов контактных напряжений Г. Герца.
Расчет ведется по расчетной окружной силе (q), отнесенной к единице ширины венца.

где: P – передаваемое окружное усилие;
b – ширина венца зубчатого колеса (длина зуба);
K – коэффициент нагрузки, учитывающий дополнительные вредные явления (удары).
q – расчетная окружная сила, отнесенная к единице ширины венца (b).
Нормальная удельная сила равна:

Перенесем силу давления qn вдоль линии ее действия (линия зацепления) в точку, расположенную на оси симметрии зуба (рис. 13.4) и разложим на две составляющие: изгибающую зуб (qncosαn), вызывающую в опасном сечении напряжения изгиба (σu) и сжимающую зуб (qnsinα), вызывающую в зубе напряжения сжатия (σcж). Угол «γ» несколько больше угла профиля «αw» (γ = αw = 20˚).
Номинальное напряжение в опасном сечении:

;

;

;

;

;

;

.
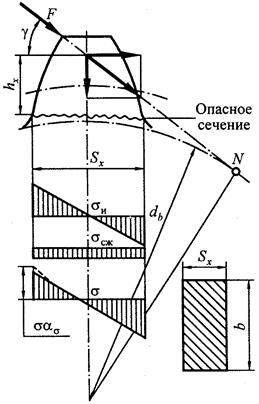
Рис. 13.4. Схема расчета зубьев на изгиб
Умножим числитель и знаменатель на модуль «m» и заменим 
получим:

,

,

;
приняв: 
;
получим: 
.

;

обозначив: 
получим: 
,
где: KT – теоретический коэффициент концентрации напряжений;
YFHU, YF – коэффициенты прочности зубьев соответственно по номинальным и местным напряжениям;
YFH – представляет собой номинальное напряжение в опасном сечении зуба при m = 1 и q = 1, а YF – местное напряжение при тех же условиях.
Технические расчеты удобно вести по формулам, в которых условия нагружения заданы в форме номинальных крутящих моментов М (ктс.см) или мощности (кВт), частоты вращения n (об/мин) и коэффициента нагрузки К.

;
Для технических проверочных расчетов следует умножить P.K и приняв

получим: 
;
если 
то: 
.
Модуль и ширина зубчатого венца, прежде всего, определяют прочность зуба на изгиб. Приняв 
и решив последнее уравнение относительно модуля, после преобразований получим:

.
Наиболее рациональной формой расчет, обеспечивающей равнопрочностъ зубьев по выкрашиванию и излому, является определение модуля по известному межосевому расстоянию “aw” и ширине зубчатого венца “b” полученным из расчета на конкретную прочность.

.
После преобразования получим:

,

.
Для большинства редукторов общего назначения:

;
коэффициент нагрузки К можно выразить:

,
здесь: Kβ – коэффициент концентрации нагрузки;
Kv – коэффициент динамичности нагрузки.
Чтобы нарезать зубчатое колесо, надо знать элементы зубчатого зацепления, т. е. число зубьев, шаг зубьев, высоту и толщину зуба, диаметр делительной окружности и наружный диаметр. Эти элементы показаны на рис. 240.

Рассмотрим их последовательно.
В каждом зубчатом колесе различают три окружности и, следовательно, три соответствующих им диаметра:
во-первых, окружность выступов, которая представляет собой наружную окружность заготовки зубчатого колеса; диаметр окружности выступов, или наружный диаметр, обозначается Dе;
во-вторых, делительную окружность, которая представляет собой условную окружность, делящую высоту каждого зуба на две неравные части — верхнюю, называемую головкой зуба, и нижнюю, называемую ножкой зуба; высота головки зуба обозначается h', высота ножки зуба — h"; диаметр делительной окружности обозначается d;
в-третьих, окружность впадин, которая проходит по основанию впадин зуба; диаметр окружности впадин обозначается Di.
Расстояние между одноименными (т. е. обращенными в одну сторону, например двумя правыми или двумя левыми) боковыми поверхностями (профилями) двух смежных зубьев колеса, взятое по дуге делительной окружности, называется шагом и обозначается t. Следовательно, можно записать:

где t — шаг в мм;
d — диаметр делительной окружности;
z — число зубьев.
Модулем m называется длина, приходящаяся по диаметру делительной окружности на один зуб колеса; численно модуль равен отношению диаметра делительной окружности к числу зубьев. Следовательно, можно записать:

Из формулы (10) следует, что шаг
t = πm = 3,14m мм. (9б)
Чтобы узнать шаг зубчатого колеса, надо его модуль умножить на π.
В практике нарезания зубчатых колес наиболее важным является модуль, так как все элементы зуба связаны с велининой модуля.
Высота головки зуба h' равна модулю m, т. е.
h' = m. (11)
Высота ножки зуба h" равна 1,2 модуля, или
h" = 1,2m. (12)
Высота зуба, или глубина впадины,
h = h' + h" = m + 1,2m = 2,2m. (13)
По числу зубьев z зубчатого колеса можно определить диаметр его делительной окружности.
d = z · m. (14)
Наружный диаметр зубчатого колеса равен диаметру делительной окружности плюс высота двух головок зуба, т. е.
De = d + 2h' = zm + 2m = (z + 2)m. (15)
Следовательно, для определения диаметра заготовки зубчатого колеса надо число его зубьев увеличить на два и полученное число умножить на модуль.
В табл. 16 даны основные зависимости между элементами зубчатого зацепления для цилиндрического колеса.

Пример 13. Определить все размеры, необходимые для изготовления зубчатого колеса, имеющего z = 35 зубьев и m = 3.
Определяем по формуле (15) наружный диаметр, или диаметр заготовки:
De = (z + 2)m = (35 + 2) · 3 = 37 · 3 = 111 мм.
Определяем по формуле (13) высоту зуба, или глубину впадины:
h = 2,2m = 2,2 · 3 = 6,6 мм.
Определяем по формуле (11) высоту головки зуба:
h' = m = 3 мм.
Зуборезные фрезы
Для фрезерования зубчатых колес на горизонтально-фрезерных станках применяют фасонные дисковые фрезы с профилем, соответствующим впадине между зубьями колеса. Такие фрезы называют зуборезными дисковыми (модульными) фрезами (рис. 241).

Зуборезные дисковые фрезы подбирают в зависимости от модуля и числа зубьев фрезеруемого колеса, так как форма впадины двух колес одного и того же модуля, но с разным числом зубьев неодинакова. Поэтому при нарезании зубчатых колес для каждого числа зубьев и каждого модуля следовало бы иметь свою зуборезную фрезу. В условиях производства с достаточной степенью точности можно пользоваться несколькими фрезами для каждого модуля. Для нарезания более точных зубчатых колес необходимо иметь набор из 15 зуборезных дисковых фрез, для менее точных достаточен набор из 8 зуборезных дисковых фрез (табл 17).
15-штучный набор зуборезных дисковых фрез
| Номер фрезы | 1 | 1½ | 2 | 2½ | 3 | 3½ | 4 | |
| Число зубьев на- резаемого ко- леса | 12 | 13 | 14 | 15-16 | 17-18 | 19-20 | 21-22 | |
| Номер фрезы | 4½ | 5 | 5½ | 6 | 6½ | 7 | 7½ | 8 |
| Число зубьев на- резаемого ко- леса | 23-25 | 26-29 | 30-34 | 35-41 | 42-54 | 55-79 | 80-134 | 135 рейка |
8-штучный набор зуборезных дисковых фрез
| Номер фрезы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Число зубьев на- резаемого ко- леса | 12-13 | 14-16 | 17-20 | 21-25 | 26-34 | 35-54 | 55-134 | 135 рейка |
В целях сокращения количества размеров зуборезных фрез в Советском Союзе модули зубчатых колес стандартизованы, т. е. ограничены следующими модулями: 0,3; 0,4; 0,5; 0,6; 0,75; 0,8; 1,0; 1,25; 1,5; 1,75; 2,0; 2,25; 2,50; 3,0; 3,5; 4,0; 4,5; 5,0; 5,5; 6,0; 6,5; 7,0; 8,0; 9,0; 10,0; 11; 12; 13; 14; 15; 16; 18; 20; 22; 24; 26; 28; 30; 33; 36; 39; 42; 45; 50.
На каждой зуборезной дисковой фрезе выбиты все характеризующие ее данные, позволяющие правильно произвести выбор необходимой фрезы.
Зуборезные фрезы изготовляют с затылованными зубьями. Это — дорогой инструмент, поэтому при работе с ним необходимо строго соблюдать режимы резания.
Измерение элементов зуба
Измерение толщины и высоты головки зуба производится зубомером или штангензубомером (рис. 242); устройство его измерительных губок и метод отсчета по нониусу подобны прецизионному штангенциркулю с точностью 0,02 мм.

Величина А, на которую следует установить ножку 2 зубомера, будет:
А = h' · а = m · а мм, (16)
где m — модуль измеряемого колеса.
Коэффициент а всегда больше единицы, так как высота головки зуба h' измеряется по дуге начальной окружности, а величина А измеряется по хорде начальной окружности.
Величина В, на которую следует установить губки 1 и 3 зубомера, будет:
В = m · b мм, (17)
где m — модуль измеряемого колеса.
Коэффициент b учитывает, что размер В — это размер хорды по начальной окружности, в то время как ширина зуба равна длине дуги начальной окружности.
Значения а и b даны в табл. 18.
Так как точность отсчета штангензубомера составляет 0,02 мм, то у полученных по формулам (16) и (17) величин отбрасываем третий десятичный знак и округляем до четных значений.
Значения a и b для установки штангензубомера
| Число зубьев измеряемого колеса | Значения коэффициентов | Число зубьев измеряемого колеса | Значения коэффициентов | ||
| a | b | a | b | ||
| 12 | 1,0513 | 1,5663 | 27 | 1,0228 | 1,5698 |
| 13 | 1,0473 | 1,5669 | 28 | 1,0221 | 1,5699 |
| 14 | 1,0441 | 1,5674 | 29 | 1,0212 | 1,5700 |
| 15 | 1,0411 | 1,5679 | 30 | 1,0206 | 1,5700 |
| 16 | 1,0385 | 1,5682 | 31-32 | 1,0192 | 1,5701 |
| 17 | 1,0363 | 1,5685 | 33-34 | 1,0182 | 1,5702 |
| 18 | 1,0342 | 1,5688 | 35 | 1,0176 | 1,5702 |
| 19 | 1,0324 | 1,5690 | 36 | 1,0171 | 1,5703 |
| 20 | 1,0308 | 1,5692 | 37-38 | 1,0162 | 1,5703 |
| 21 | 1,0293 | 1,5693 | 39-40 | 1,0154 | 1,5704 |
| 22 | 1,0281 | 1,5694 | 41-42 | 1,0146 | 1,5704 |
| 23 | 1,0268 | 1,5695 | 43-44 | 1,0141 | 1,5704 |
| 24 | 1,0257 | 1,5696 | 45 | 1,0137 | 1,5704 |
| 25 | 1,0246 | 1,5697 | 46 | 1,0134 | 1,5705 |
| 26 | 1,0237 | 1,5697 | 47-48 | 1,0128 | 1,5706 |
| 49-50 | 1,023 | 1,5707 | 71-80 | 1,0077 | 1,5708 |
| 51-55 | 1,0112 | 1,5707 | 81-127 | 1,0063 | 1,5708 |
| 56-60 | 1,0103 | 1,5708 | 128-135 | 1,0046 | 1,5708 |
| 61-70 | 1,0088 | 1,5708 | Рейка | 1,0000 | 1,5708 |
Пример 14. Установить зубомер для проверки размеров зуба колеса с модулем 5 и числом зубьев 20.
По формулам (16) и (17) и табл. 18 имеем:
А = m · а = 5 · 1,0308 = 5,154 или, округленно, 5,16 мм;
В = m · b = 5 · 1,5692 = 7,846 или, округленно, 7,84 мм.
Геометрические параметры эвольвентного зацепления
Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.
В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:
- w – начальной;
- b – основной;
- a – вершин зубьев;
- f – впадин зубьев.
Параметрам, относящимся к делительной окружности, индекс не присваивается.
При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» - колесу.
Начальные окружности
Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О1 и О2 до полюса П ) при неизменном межосевом расстоянии О1О2 тоже остается неизменным.
При изменении межосевого расстояния aw меняются и диаметры dw начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.
Межосевое расстояние определяется по формуле:

Делительная окружность
Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.
Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.
У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:
Исключение составляют передачи с угловой модификацией.
Окружной шаг зубьев
Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.
Основной шаг
Этот параметр, обозначаемый pb , относится к основной окружности. На основании второго и четвертого свойств эвольвенты расстояние по нормали между одноименными сторонами двух соседних зубьев равно шагу pb .
Из треугольника О2ВП (см. рис. 1) диаметр основной окружности db2 = 2 rb2 = d2 cos αw , откуда основной шаг может быть определен по формуле:
Окружная толщина зуба и окружная ширина впадины
Окружная толщина зуба st и окружная ширина впадины et по дуге делительной окружности колеса передачи без смещения теоретически равны. Однако при изготовлении зубчатых колес на теоретический размер st назначают такое расположение поля допуска, при котором зуб получается тоньше, чем и гарантируется боковой зазор j (рис. 1), необходимый для нормального зацепления. По делительной окружности всегда st + et = p .
Окружной модуль зубьев
Из определения окружного шага следует, что длина делительной окружности зубчатого колеса πd = pz , где z – число зубьев. Следовательно,
Шаг зубьев p , так же как длина окружности, включает в себя трансцендентное число π , а поэтом шаг - также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число p/π , которое называют модулем зубьев , обозначают m и измеряют в миллиметрах:
d = mz или m = d/z .
Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.
Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).
При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.
Высота головки и ножки зуба
Делительная окружность делит зуб по высоте на головку ha и ножку hf . Для создания радиального зазора с (см . рис. 1) необходимо
Для передачи без смещения ha = m .
Длина активной линии зацепления
При вращении зубчатых колес точка зацепления S (см. рис. 1) пары зубьев перемещается по линии зацепления NN . Зацепление профилей начинается в точке S' пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S'' пересечения линии зацепления с окружностью вершин шестерни.
Отрезок S'S'' линии зацепления называют длиной активной линии зацепления и обозначают gα . Длину gα легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S'S'' и замеряют gα .

Коэффициент торцового перекрытия
Коэффициентом торцового перекрытия εα называют отношение длины активной линии зацепления к основному шагу:
где z1 и z2 – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.
Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.
За период работ пары зубьев точка их зацепления проходит путь, равный по длине gα (см. рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу pb . При gα > pb необходимое перекрытие зубьев обеспечивается.
По условию непрерывности зацепления должно быть εα > 1. С увеличением количества зубьев z увеличивается и коэффициент торцового перекрытия εα .
Читайте также:

