Прямой зуб и косой зуб

Опубликовано: 29.04.2024

Косозубыми называются цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном цилиндре (см. рис. 11, б). Прямозубую зубчатую передачу можно рассматривать как частный случай косозубой, у которой угол наклона линии зуба колеса на делительном цилиндре β = 0 (см. рис. 11, а).

В отличие от прямозубой, в косозубой передаче зубья входят в зацепление не сразу по всей длине, а постепенно. Увеличивается время контакта одной пары зубьев, в течение которого входят новые пары зубьев, нагрузка передается по большому числу контактных линий, что значительно снижает шум и динамические нагрузки.

Чем больше угол наклона линии зуба, тем выше плавность зацепления. У пары сопряженных косозубых колес с внешним зацеплением углы β равны, но противоположны по направлению.

Основные термины, определения и обозначения параметров зубчатых передач

В обозначениях основных параметров (табл. 1), необходимых для геометрического расчета и выполнения чертежей цилиндрических зубчатых колес используют определенные индексы, значения которых таковы:

1; 2 – относящиеся соответственно к шестерне и колесу,

а – относящийся к поверхности или окружности вершин и головке зубьев;

b – относящийся к основной окружности зубчатого колеса;

f – относящийся к поверхности или окружности впадин и ножке зуба;

l – относящийся к окружности граничных точек;

п – нормальный или относящийся к нормальному сечению;

t – окружной, торцовый или относящийся к торцовому сечению;

w – относящийся к начальной поверхности или начальной окружности;

х – осевой или относящийся к осевому сечению;

у – относящийся к любой соосной поверхности или концентрической окружности.

Коэффициент, характеризующий соответствующий параметр, обозначается так же, как этот параметр, но с индексом *, а черточка над параметром означает, что данный параметр характеризует хордальный размер зубьев или расстояние до измеряемой хорды.

Основные термины, определения и обозначения параметров и элементов

цилиндрических зубчатых передач по ГОСТ 16530–83 (СТ СЭВ 3295–81)

и ГОСТ 16531–83 (СТ СЭВ 3294–81)

Определение и зависимость

Делительное межосевое расстояние

Межосевое расстояние, равное полусумме делительных диаметров зубчатых колес при внешнем или полуразности при внутреннем зацеплении (рис. 15, а)

Расстояние между осями зубчатых колес по межосевой линии (см. рис. 15, а)

Наименьшее расстояние между торцами зубьев зубчатого колеса по линии, параллельной его оси (рис. 15, б)

Продолжение табл. 1

Определение и зависимость

Общая часть ширины венцов зубчатых колес, в пределах которой глубина захода зубьев постоянна (см. рис. 15, б)

Расстояние между вершинами и впадинами зубьев пары исходных контуров, находящихся в зацеплении, при совпадении их делительных прямых

Диаметр концентрической окружности зубчатого колеса (см. рис. 15)

Диаметр окружности вершин зубьев

Диаметр окружности впадин зубьев

Диаметр окружности граничных точек

Расстояние между окружностями вершин зубьев и впадин (см. рис. 15, а)

Высоты головки и

Расстояния между делительной окружностью колеса и его окружностями вершин или впадин (см. рис. 15, а)

Граничная высота зуба

Расстояние между окружностью вершин зубьев и концентрической окружностью, проходящей через граничные точки профилей зубьев (см. рис. 15, а)

Глубина захода зубьев

Длина отрезка межосевой линии, заключенного между окружностями вершин зубьев шестерни и колеса (см. рис. 15, б)

Окружной и нормальный шаги зубьев

Расстояние между одноименными профилями соседних зубьев по дуге делительной окружности (см. рис. 15, а). Для прямозубых колес p_t = p_n

m, m_t, m_n

Расчетный, окружной и нормальный модули

Модуль – линейная величина, в π раз меньшая соответствующего шага зубчатого колеса. Для прямозубых колес m = m_t = m_n

Окружная и нормальная толщина зубьев

Расстояние между разноименными профилями зуба по дуге делительной окружности колеса (см. рис. 15, а). Для прямозубых колес

Окончание табл. 1

Определение и зависимость

Коэффициент смещения исходного контура

Отношение смещения исходного контура к расчетному модулю

Коэффициент суммы смещений

Коэффициент воспринимаемого смещения

y= (a_w – a)/m

Коэффициет уравнительного смещения

Δу= x_∑ – y

Число зубьев колеса

Угол профиля зуба

Для прямозубых колес α = α_t

Угол профиля зуба производящей рейки в

Угол зацепления в торцовом сечении

Острый угол между линией зацепления и нормалью к линии центров (см. рис. 15, а). Для прямозубых колес при β=0 α_tw = α_t

Угол наклона линии зуба колеса на делительном цилиндре

Угол между касательной к боковой поверхности зуба и образующей делительного цилиндра

Радиус кривизны переходной кривой в граничной точке профиля

Анатомия: Строение зуба (зубов)

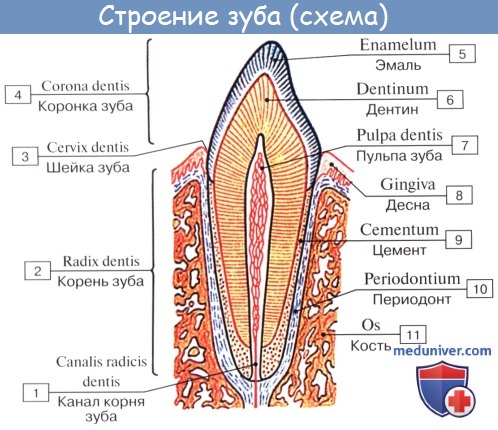
Каждый зуб, dens, состоит из:
1) коронки зуба, corona dentis,
2) шейки, collum dentis и
3) корня, radix dentis
Коронка выдается над десной, шейка (слегка суженная часть зуба) охватывается десной, а корень сидит в зубной альвеоле и оканчивается верхушкой, apex radicis, на которой даже невооруженным глазом видно маленькое отверстие верхушки —foramen apicis. Через это отверстие в зуб входят сосуды и нервы. Внутри коронки зуба имеется полость, cavitas dentis, в которой различают коронковый отдел, наиболее обширную часть полости, и корневой отдел, суживающуюся часть полости, носящую название корневого канала, canalis radicis dentis. Канал открывается на верхушке упомянутым выше отверстием верхушки. Полость зуба выполнена зубной мякотью, pulpa dentis, богатой сосудами и нервами. Зубные корни плотно срастаются с поверхностью зубных ячеек посредством альвеолярной надкостницы, periodontium, богатой кровеносными сосудами. Зуб, периодонт, стенка альвеолы и десна составляют зубной орган. Твердое вещество зуба состоит из: 1) дентина, dentinum, 2) эмали, enamelum, и 3) цемента, cementum. Главную массу зуба, окружающую полость зуба, составляет дентин. Эмаль покрывает снаружи коронку, а корень покрыт цементом.

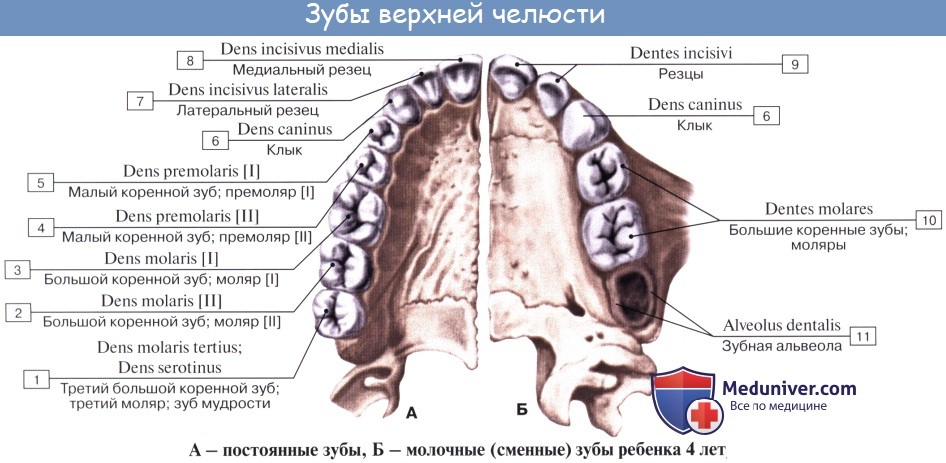
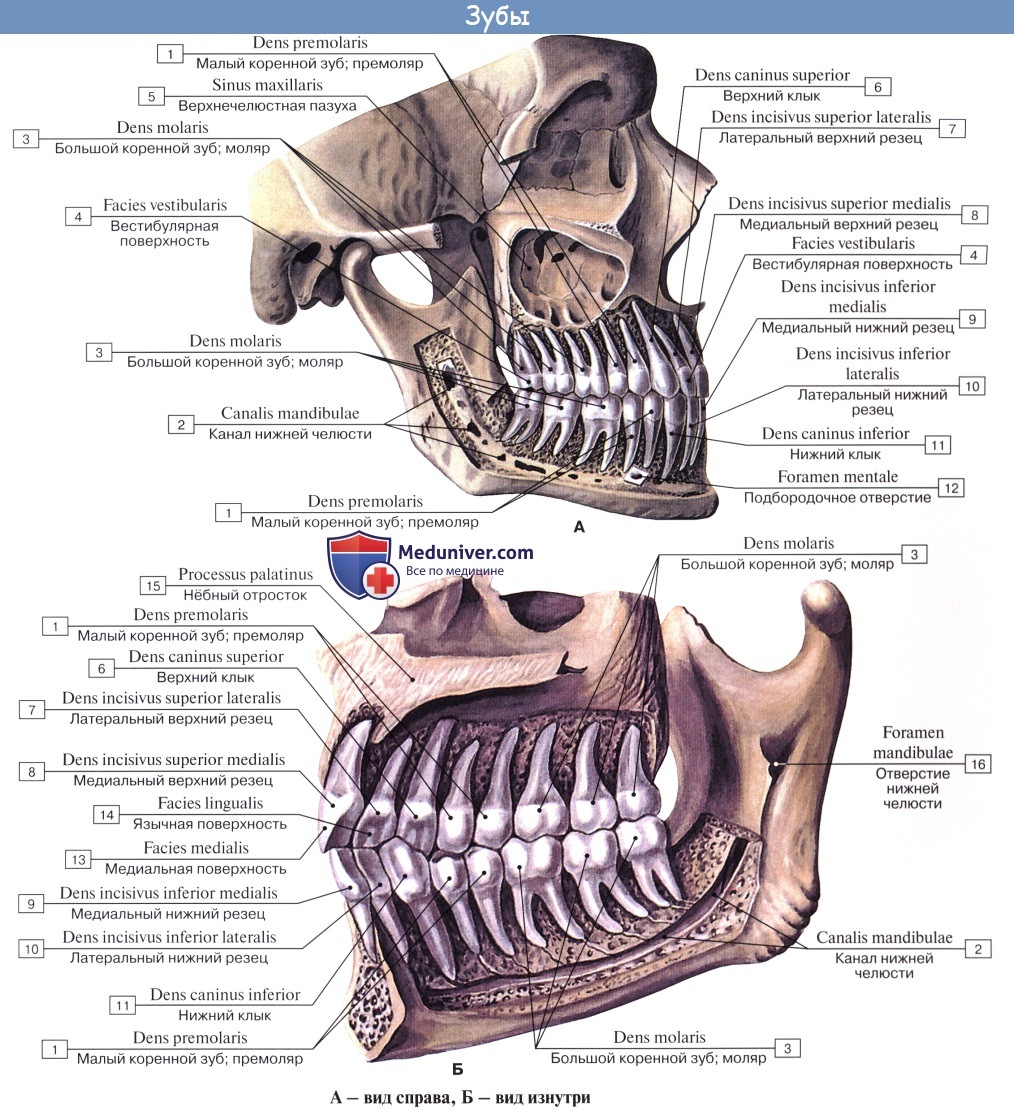
Зубы заключены в челюстях таким образом, что коронки зубов находятся снаружи и образуют зубные ряды — верхний и нижний. Каждый зубной ряд содержит по 16 зубов, расположенных в виде зубной дуги.

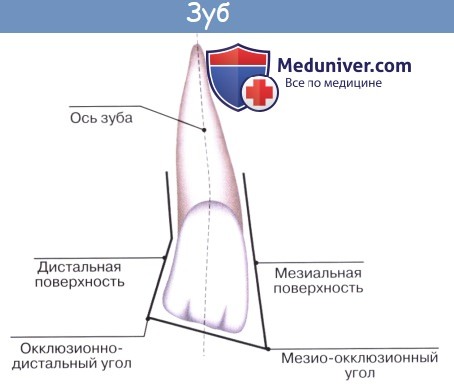
В каждом зубе различают 5 поверхностей:
1) обращенную в преддверие рта, facies vestibularis, которая у передних зубов соприкасается со слизистой губы, а у задних — со слизистой щеки;
2) обращенную в полость рта, к языку, facies lingualis;
3 и 4) контактирующие с соседними зубами своего ряда, facies contactus.
Контактные поверхности зубов, направленные к центру зубной дуги, обозначаются как facies mesialis (meso, греч. — между). У передних зубов такая поверхность является медиальной, а у задних зубов — передней. Контактные поверхности зубов, направленные в сторону, противоположную центру зубного ряда, называются дистальными, facies distalis. У передних зубов эта поверхность является латеральной, а у задних зубов — задней; 5) жевательную поверхность, или поверхность смыкания с зубами противоположного ряда, facies occlusalis.

Для определения локализации патологических процессов на зубе стоматологи применяют термины, соответствующие названным поверхностям: вести-булярно, орально, медиально, мезиально, дистально, окклюзиально, апи-кально (по направлению к apex radicis).

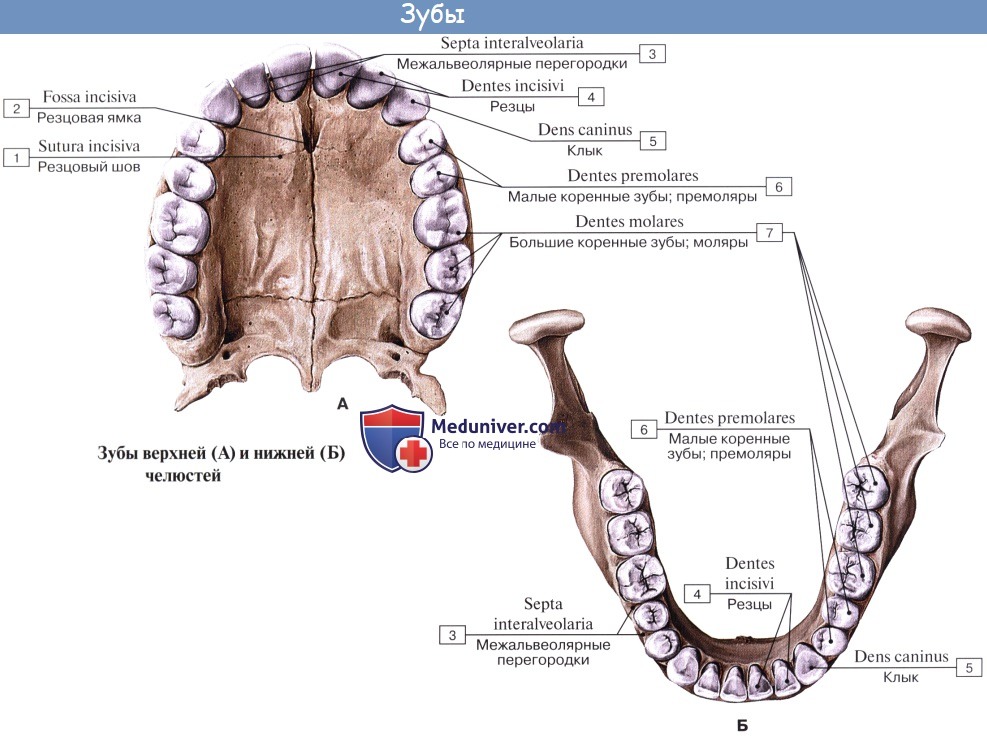
Для установления принадлежности зуба к правой или левой стороне служат три признака:
1) признак корня,
2) признак угла коронки и
3) признак кривизны коронки.

Признак корня заключается в том, что продольная ось корня наклонена в дистальную сторону, образуя угол с линией, проходящей через середину коронки.

Признак угла коронки состоит в том, что линия жевательного края зуба по вестибулярной стороне при переходе на мезиальную поверхность образует меньший угол, чем при переходе на дистальную.

Признак кривизны коронки состоит в том, что вестибулярная поверхность коронки переходит в мезиальную более круто, чем в дистальную. Следовательно, мезиальный отрезок вестибулярной поверхности в поперечном направлении будет более выпуклым, чем дистальный. Это объясняется тем, что мезиальный отдел коронки развит более мощно, чем дистальный. Образуется мезиодистальный скат вестибулярной поверхности коронки.

Принадлежность отдельно взятого зуба к верхней или нижней челюсти определяется формой коронки, а также формой и числом корней. Поэтому необходимо знать форму коронки и число корней не только для определенных групп зубов, но и для каждого отдельного зуба данной группы.

Какова разница между червячной, конической, косозубой и прямозубой передачей?

Зубчатая передача — это наиболее важная часть многих механизмов и двигателей. Их наличие помогает увеличить выходной крутящий момент за счет обеспечения необходимого передаточного числа и позволяет регулировать направление движения выходного вала, например, приводного вала автомобиля. Ниже перечислены основные типы передач (шестерен) и рассмотрены их отличия друг от друга.

• Прямозубая передача
  

Косозубые передачи позволяют добиться плавной работы благодаря постоянному контакту расположенных под углом зубьев.

Зубчатые колеса прямозубых передач монтируются последовательно на параллельных валах и позволяют достичь больших значений передаточного отношения.

Наиболее распространены прямозубые передачи, которые используются для обеспечения больших передаточных отношений. Зубья колес в таких передачах расположены под прямым углом, а сами зубчатые колеса установлены на параллельных валах. Прямозубые передачи используются в стиральных машинах, шуруповертах, заводных будильниках и прочих устройствах. Эти передачи довольно шумны вследствие механического столкновения зубчатых колес в момент вхождения в зацепление. Каждое зацепление вызывает громкий шум и вибрацию, именно поэтому прямозубые передачи не используются в сложной технике, такой как автомобили. Обычно передаточное число таких механизмов варьируется от 1:1 до 6:1.

• Косозубая передача
  

На вышеприведенном рисунке изображены два различных типа конических передач: прямозубая и спиральнозубая.

Косозубые передачи работают более плавно и тихо в сравнении с прямозубыми благодаря особому типу контакта зубьев. Зубья в данном случае расположены под углом к поверхности шестерни. Когда два зуба шестерен входят в зацепление, контакт между ними устанавливается постепенно, начиная с одного конца зуба. Контакт поддерживается на протяжении всего цикла зацепления. Зубья обычно расположены под углом от 15 до 30 градусов. Осевая нагрузка напрямую зависит от величины угла наклона зубьев. Косозубые передачи наиболее часто применяются в коробках передач. Они генерируют достаточно большую нагрузку, для восприятия которой используются упорные подшипники. Также косозубые передачи могут использоваться для передачи крутящего момента в случае, если зубчатые колеса устанавливаются под углом 90 градусов на перпендикулярных валах. Передаточное число обычно варьируется от 3:2 до 10:1.

• Конические передачи
  

Конические передачи обычно используются для передачи вращения вала в другом направлении. Зубья конической передачи могут быть прямой, спиральной или гипоидной формы. Шестерни с прямыми зубьями имеют те же характеристики, что и шестерни прямой передачи, и также подвержены высоким нагрузкам в момент зацепления. Прямозубые конические передачи, как и прямозубые цилиндрические передачи, имеют передаточные числа от 3:2 до 5:1.

В данном двигателе используется редуктор, состоящий из гипоидных и спиральнозубых конических зубчатых колес.

На вышеприведенном рисунке показан вид двигателя в разрезе, иллюстрирующий работу спиральнозубой конической передачи.

Спиральнозубые шестерни функционально не отличаются от косозубых шестерен. Они обеспечивают низкие уровни шумов и вибраций в сравнении с прямозубыми шестернями. Спиральнозубые шестерни, имеющие зубья с правым наклоном, используются для вращения по часовой стрелке относительно оси. Шестерни с левым наклоном используются для вращения против часовой стрелки относительно оси. Передаточное число таких передач варьируется от 3:2 до 4:1.

В гипоидной передаче, изображенной выше, большое зубчатое колесо называется ведомым, а меньшее — ведущим.

Гипоидная передача является разновидностью спиральной передачи, в которой зубчатые колеса имеет не коническую, а гиперболоидную форму. В гипоидной передаче ведущее зубчатое колесо располагается эксцентрично относительно ведомого. Это позволяет использовать ведущую шестерню большего диаметра и обеспечивает большую площадь пятна контакта.

Ведущее и ведомое колеса всегда вращаются в противоположные стороны, а спиральный угол зубьев ведущего колеса обычно больше угла зубьев ведомого. Благодаря большему передаточного числу, которое варьируется от 10:1 до 200:1, гипоидная передача широко используется в силовых трансмиссиях.

• Червячная передача

На рисунке изображена червячная передача в разрезе, что позволяет понять не только ее устройство, но и принцип работы. Особенности конструкции червячной передачи исключают ее вращение в обратном направлении.

Червячная передача используется в редукторах с большим передаточным числом, которое варьируется от 5:1 до 300:1. Пара конструктивно выполнена таким образом, чтобы червяк был в состоянии крутить шестерню, но шестерня не могла приводить в движение червяк. Угол подъема витка червяка является пологим, в результате чего шестерня удерживается на месте благодаря трению, возникающему при зацеплении. Червячные передачи используются в таком оборудовании как конвейеры, где блокировка обратного движения выполняет функцию тормоза или аварийного останова.

2015-02-24
20930

Косозубые зубчатые передачи, как и прямозубые, предназначены для передачи вращательного момента между параллельными валамя (рис. 36). У косозубых колес оси зубьев располагаются не по образующей делитель­ного цилиндра, а по винтовой линии, составляющей с образующей угол (рис. 37). Угол наклона зубьев р принимают равным , он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.

Рис. 36. Цилиндрическая косозубая передача

Передаточное число для одной пары колес может быть . В прямозубых передачах линия контакта параллельна оси, а в косозубых расположена по диа­гонали на поверхности зуба (контакт в прямозубых передачах осуществляется вдоль всей длины зуба, а в косозубых — сначала в точке увеличивается до пря­мой, «диагонально» захватывающей зуб, и постепен­но уменьшается до точки).

Достоинства косозубых передач по сравнению с прямозубыми: уменьшение шума при работе; меньшие габаритные размеры; высокая плавность зацепления; большая нагрузочная способность; значительно меньшие дополнительные дина­мические нагрузки.

За счет наклона зуба в зацеплении косозубой передачи появляется осевая сила.

Направление осевой силы зависит от на­правления вращения колеса (рис. 37), на­правления винтовой линии зуба, а также от того, каким является колесо — ведущим или ведомым. Осевая сила дополнительно нагру­жает валы и опоры, что является недостатком косозубых передач.

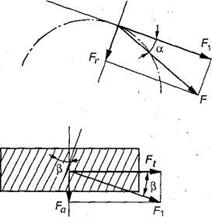
Рис. 37. Усилия в косозубой цилиндрической передаче

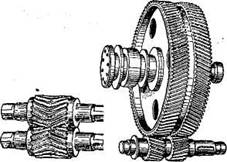
Шевронные зубчатые колеса пред­ставляют собой разновидность косозубых колес (рис. 38).

А) б)

Рис. 38. Шевронная зубчатая передача

Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (рис. 38, а), называют шеврон­ным колесом. Часть венца зубчатого колеса, в пределах которого линии зубьев имеют одно направление, называют полушевроном. Различают шев­ронные колеса с жестким углом (рис. 38, б), предназначенным для выхо­да режущего инструмента при нарезании зубьев. Шевронные передачи об­ладают всеми преимуществами косозубых, а осевые силы (рис. 39) проти­воположно направлены и на подшипник не передаются.

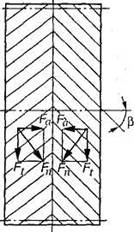
Рис.39. Усилия в зацеплении шевронных зубчатых колес

В этих передачах допускают большой угол наклона зубьев ( ). Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т.е. в тех случаях, когда требует­ся передавать большую мощность и высокую скорость, а осевые нагрузки нежелательны.

Рис. 40

Косозубые и шевронные колеса в отличие от прямозубых имеют два шага и два модуля: в нормальном сечении (см. рис. 44) по делительной окружности — нормальный шаг р_п, в торцовой плоскости — торцовый шаг р_t. Из условия, что модуль зацепления равен шагу, деленному на число , имеем ; .

Для косозубых и шевронных колес значения нормального модуля т_n стандартизованы, так как профиль косого зуба в нормальном сечении со­ответствует исходному контуру инструментальной рейки и, следовательно, т = т_п (косозубые и шевронные колеса нарезают, тем же способом и инст­рументом, что и прямозубые). Нормальный модуль т_п является исходным при геометрических расчетах.

Определим зависимость между нормальным и торцовым шагом и модулем через угол наклона зубьев.

Если левую и правую части разделим на , получим

Геометрические параметры цилиндрической косозубой и шевронной передач с эвольвентным профилем зуба рассчитают по формулам, приве­денным в табл. 15. По торцовому модулю т_t рассчитывают делительные (начальные) диаметры, а до т_п — все остальные размеры зубчатых колес.

Таблица 15. Геометрические параметры цилиндрической косозубой передачи

Параметр, обозначение	Расчетные формулы
Нормальный модуль
Торцовый (окружной модуль)
Диаметр вершин зубьев в
Делительный диаметр d
Диаметр впадин зубьев
Шаг нормальный
Шаг торцовый (окружной)
Окружная толщина зубьев
Ширина впадин зубьев
Высота зуба
Высота головки зуба
Высота ножки зуба
Радиальный зазор
Межосевое расстояние
Длина зуба
Ширина венца

Окружная сила . На косой зуб действует осевая сила (см. рис. 37), радиальная (распорная) сила .

В косозубдй передаче сила , действующая на зуб косозубого колеса (см. рис. 44), направлена по нормали к профилю зуба, т.е. по линии зацепле­ния эквивалентного прямозубого колеса, и составляет угол с касательной к
эллипсу.

Эту силу разложим на две составляющие: окружную силу на эквива­лентном колесе и радиальную (распорную) силу на этом колесе .

Если, в свою очередь, силу разложить по двум направлениям, то по­лучим такие силы: — окружную силу, — осевую.

Для зубчатого колеса с шевронным зубом окружную силу и рас­порную определяют по тем же формулам, что и для косозубой передачи т.е. , . В шевронной передаче осевая сила (см. рис. 39).

Винтовая передача (разновидность ко­созубой) состоит из двух косозубых цилиндри­ческих колес (рис. 41). Однако в отличие от косозубых цилиндрических передач с парал­лельными валами касания между зубьями здесь происходит в точке и при значительных скоро­стях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.

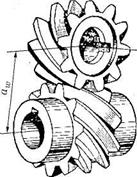
Рис.41. Винтовая зубчатая передача

Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. При проектировании зубчатого колеса вначале нужно определить его число зубьев z , а затем определить параметры зубьев. Для этого нужно произвольную окружность колеса r y разделить на z частей, каждая из которых называется окружным шагом p y .

где m y = p y / p = d y / z - модуль зацепления по окружности произвольного радиуса.

Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p . В зависимости от окружности по которой определен модуль различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) - число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого модуль можно определить как число милиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по окружности называемой делительной. Точнее делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба). Угловой шаг t - центральный угол соответствующий дуге p - окружному шагу по делительной окружности.

Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины - строчными буквами латинского алфавита, угловые - греческими буками; установлены индексы для величин :

по окружностям: делительной - без индекса, вершин - a , впадин - f , основная - b , начальная - w , нижних точек активных профилей колес - p , граничных точек - l ;

по сечениям: нормальное сечение - n , торцевое сечение - t , осевое сечение - x ;

относящихся к зуборезному инструменту - 0 .

Для параметров зубчатого колеса справедливы следующие соотношения

- диаметр окружности произвольного радиуса,

- диаметр делительной окружности,

- шаг по окружности произвольного радиуса,

- шаг по делительной окружности,

где a - угол профиля на делительной окружности,

a y - угол профиля на окружности произвольного радиуса.

Углом профиля называется острый угол между касательной к профилю в данной точки и радиусом - вектором, проведенным в данную точку из центра колеса.

Шаг колеса делится на толщину зуба s y и ширину впадины e y . Толщина зуба s y - расстояние по дуге окружности r y между разноименными точками профилей зуба. Ширина впадины e y - расстояние по дуге окружности r y между разноименными точками профилей соседних зубьев.

На основной окружности a b => 0 и cos a b => 1 , тогда

В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:

нулевые s = e = p * m / 2 , D = 0;

положительные s > e , => D > 0;

отрицательные s D D - коэффициент изменения толщины зуба (отношение приращения толщины зуба к модулю). Тогда толщину зуба по делительной окружности можно записать

Более подробно познакомиться с основными определениями и расчетными зависимостями можно в литературе [ 11.1 ] и в ГОСТ 16530-83.

Толщина зуба колеса по окружности произвольного радиуса .

Толщина зуба по дуге делительной окружности

Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 12.2

Подставляя в формулу угловой толщины эти зависимости, получим

Методы изготовления эвольвентных зубчатых колес .

Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода:

метод копирования, при котором рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности ( конгруентны ей, т. е. заполняют эту поверхность как отливка заполняет форму );

метод огибания, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения - резания и огибания (под огибанием понимается такое относительное движение заготовки и инструмента , которое соответствует станочному зацеплению , т. е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения).

Из вариантов изготовления по способу копирования можно отметить:

Нарезание зубчатого колеса профилированной дисковой или пальцевой фрезой (проекция режущих кромок которой соответствует конфигурации впадин). При этом методе резание производится в следующем прядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются пока не будут прорезаны все впадины. Производительность данного способа низкая, точность и качество поверхности невысокие.

Отливка зубчатого колеса в форму. При этом внутренняя поверхность литейной формы конгруентна наружной поверхности зубчатого колеса. Производительность и точность метода высокая, однако при этом нельзя получить высокой прочности и твердости зубьев.

Из вариантов изготовления по способу огибания наибольшее распространение имеют:

Обработка на зубофрезерных или зубодолбежных станках червячными фрезами или долбяками. Производительность достаточно высокая, точность изготовления и чистота поверхностей средняя. Можно обрабатывать колеса из материалов с невысокой твердостью поверхности.

Накатка зубьев с помощью специального профилированного инструмента. Обеспечивает высокую производительность и хорошую чистоту поверхности. Применяется для пластичных материалов, обычно на этапах черновой обработки. Недостаток метода образование наклепанного поверхностного слоя, который после окончания обработки изменяет свои размеры.

Обработка на зубошлифовальных станках дисковыми кругами. Применяемся как окончательная операция после зубонарезания (или накатки зубьев) и термической обработки. Обеспечивает высокую точность и чистоту поверхности. Применяется для материалов с высокой поверхностной прочностью.

Понятие о исходном, исходном производящем и производящем контурах .

Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются:

для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения - исходный контур;

для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения - исходный производящий контур.

По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими:

угол главного профиля a = 20 ° ;

коэффициент высоты зуба h * a = 1 ;

коэффициент высоты ножки h * f = 1.25 ;

коэффициент граничной высоты h * l = 2 ;

коэффициент радиуса кривизны переходной кривой r * f =с * /(1-sin a )= 0.38 ;

коэффициент радиального зазора в паре исходных контуров с * = 0.25.

Исходный производящий контур отличается от исходного высотой зуба h 0 = 2.5m.

Исходный и исходный производящий контуры образуют между собой конруентную пару (рис. 12.3), т.е. один заполняет другой как отливка заполняет заготовку (с радиальным зазором с * Ч m в зоне прямой вершин зуба исходной рейки). Принципиальное отличие этих контуров в том, что исходный контур положен в основу стандартизации зубчатых колес, а исходный производящий - в основу стандартизации зуборезного инструмента. Оба эти контура необходимо отличать от производящего контура - проекции режущих кромок инструмента на плоскость перпендикулярную оси заготовки.

Станочное зацепление .

Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4.

Линия станочного зацепления - геометрическое место точек контакта эвольвентной части профиля инструмента и эвольвентной части профиля зуба в неподвижной системе координат.

Смещение исходного производящего контура x*m - кратчайшее расстояние между делительной окружностью заготовки и делительной прямой исходного производящего контура.

Уравнительное смещение D y*m - условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора).

Окружность граничных точек r l - окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой.

Основные размеры зубчатого колеса .

Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).

Радиус окружности вершин

Радиус окружности впадин

Толщина зуба по делительной окружности.

Так как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать

Виды зубчатых колес (Классификация по величине смещения) .

В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением.

Подрезание и заострение зубчатого колеса .

Если при нарезании зубчатого колеса увеличивать смещение, то основная и делительная окружность не изменяют своего размера, а окружности вершин и впадин увеличиваются. При этом участок эвольвенты, который используется для профиля зуба, увеличивает свой радиус кривизны и профильный угол. Толщина зуба по делительной окружности увеличивается , а по окружности вершин уменьшается.

На рис. 12.7 изображены два эвольвентных зуба для которых

Для термобработанных зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба является нежелательным. Термообработка зубьев (азотирова-ние, цементация, цианирование), обеспечивающая высо Рис. 12.7 кую поверхностную прочность и твердость зубьев при сохранении вязкой серцевины, осуществляется за счет насыщения поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса, насыщаются углеродом больше. Поэтому после закалки они становятся более твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин зубьев меньших некоторых допустимых значений. То есть заостренным считается зуб у которого

При этом удобнее пользоваться относительными величинами [s a /m ]. Обычно принимают следующие допустимые значения

улучшение, нормализация [s a /m ] = 0.2;

цианирование, азотирование [s a /m ] = 0.25. 0.3;

цементация [s a /m ] = 0.35. 0.4.

Подрезание эвольвентных зубьев в станочном зацеплении

В процессе формирования эвольвентного зуба по способу огибания, в зависимости от взаимного расположения инструмента и заготовки возможно срезание эвольвентной части профиля зуба той частью профиля инструмента, которая формирует переходную кривую. Условие при котором это возможно определяется из схемы станочного зацепления. Участок линии зацепления, соответствующий эвольвентному зацеплению определяется отрезком B 1 . где точка B l определяется пересечением линии станочного зацепления и прямой граничных точек инструмента. Если точка B l располагается ниже (см. рис.12.8) точки N , то возникает подрезание зуба. Условие при котором нет подрезания можно записать так

Читайте также:

  
• Как влияет железо на зубы
  
• Почему зубы становятся мягкими
  
• На передних зубах ямки
  
• Отек после пластики десны
  
• Исследование кровообращения в пульпе зуба называется